Binomial Theorem

What is a Binomial Theorem?

It is a method of expanding an expression that has been raised to any finite power. A Binomial Theorem describes the algebraic expansion of powers of a binomial.
 

Who developed the Binomial Theorem?

The Binomial Theorem has been around since ancient times. In the 4th century B.C, Greek mathematician Euclid gave a special case of this theorem. Most significant contribution to the theorem was given by Persian mathematician Al-Karaji, who explained the binomial coefficient using the triangle pattern and also proved the binomial theorem and Pascal’s triangle.
 

What is the definition of Binomial in math? Explain Binomial Expression?

In algebra, binomial means a polynomial which is the sum of two terms, each of which is a monomial. So, the binomial is an algebraic expression containing two different terms. Different terms here means that the two terms should have different variables or different powers on its variable.

 

The Binomial Theorem is as follows:


 

What is (a + b)n?

In (a + b)n, a + b is the binomial. The expansion of (a + b)n can be calculated easily using binomial theorem. Let’s first understand the binomial theorem from the basic level. Let us understand how the formula for binomial expansion is derived.



If we examine the expansion of (a + b) for different exponents, we deduce that:
For (a + b)0 = 1
For (a + b)1 = a + b
For (a + b)2 = a2 + 2ab + b2
For (a + b)3 = a3 + 3a2b + 3ab2 + b3
For (a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4
 

How many terms are there in the expansion of (x + y + z + w)10?

This problem is an expansion of quadrinomial or a polynomial with four terms. To understand this concept, we will have to look at an important property of binomial theorem. It says that, the sum of the powers of its variables on any term is equals to n, where n is the exponent on (x + y).

Thus, if we see the expansion of (x + y)n
(x + y)n = nC0xn + nC1xn-1y + nC2xn-2y2 + … + nCrxn-ryr + … + nCnxn-nyn.
Here, we see that in every permutation the power n is being distributed to the variables x and y. Therefore, this distribution can be related with the coin – beggar’s method of permutation and combination.
As per the coin – beggar’s method, the number of ways to distribute n identical coins to p beggars will be n + p -1Cp-1.
In our problem, number of coins is the exponent and the number of beggar’s is the number of terms in the polynomial.
Thus for (x + y + z + w)10, we have, n = 10 and p = 4
So, the number of terms in its expansion will be = 10+4–1C4-1 = 13C3
 

What is the binomial coefficient?

In (a + b)2 = 1a2 + 2ab + 1b2
In this equation 1, 2 and 1 are called as the binomial coefficients of a2, ab and b2 respectively.
Similarly, in (a + b)3 = 1a3 + 3a2b + 3ab2 + 1b3
1, 3, 3 and 1 are called as the binomial coefficients of a3, a2b, ab2 and b3 respectively.
 

How do you use Pascal’s triangle?

Named after French mathematician Blaise Pascal, the triangle is a triangular arrangement of binomial coefficients for the expansion of different powers.
Below is the Pascal’s triangle for expansion till the exponent five.

The first and second row are the binomial coefficients for the expansion of (x + y) with the exponent 0 and 1 respectively. Each element in this triangle is the sum of the upper two elements.
 

What is the binomial series?

It is a special series, also known as Maclaurin series in mathematics.
Here x = 1 and y = x

Binomial Series:

(1 + x)n = nC0 + nC1x + nC2x2 + …… nCrxr + …. + nCnxn
The series can be converging or diverging depending upon the values of x and n.
 

How to apply Binomial Theorem if n is negative or fractional?

The Binomial Theorem for the expansion of (x + y)n where n E I+ will be: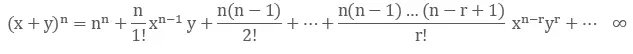

The general term will be as follows:
Note: In this case, we can’t find the binomial coefficients using nCr directly, as this is not defined for negative n.
For (a + x)n where n E I+,

In this case, where n is non positive integer, the series will converge only for (x/a) <1. But at the same time, the number of terms will be infinite i.e., infinite series.
Similarly for (1 + x)n where n E I+,

Above series converges for |x| < 1
 

How to find the term independent of x?

Here the term independent of ‘x’ means that term in the binomial expansion does not have any variable x involved in it.
This can be understood with the following example:
(x + y)2 = x2 + 2xy + y2, the third term that is, y2 is the term independent of ‘x’, while the first term that is, x2 is the term independent of y.
 

FAQ

Is binomial theorem important for JEE?

Binomial Theorem is an algebraic expression that consists of two different terms and is an important chapter for the JEE Advanced examination.
 

Is binomial distribution in JEE?

Yes, Binomial Distribution is an important topic in the Mathematics syllabus of JEE.
 

How many questions come from binomial theorem in JEE MAINS?

1-2 questions are asked from this chapter every time.
 

Is binomial theorem difficult for JEE?

It is complex at first, but becomes easy to understand once the main derivation is understood with the help of certain expansion patterns.
 

Is binomial theorem in JEE Advanced syllabus?

Binomial theorem is one of the most important chapters in the Mathematics syllabus of JEE Advanced.